Правила форума
ArcSin (функция) (пример программы)
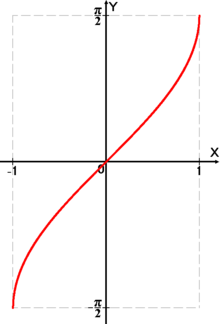
Для вычисления арксинуса в Паскале нет стандартной функции, зато его можно выразить через арктангенс. Чтобы найти ArcSin(X), нужно сначала по формуле Пифагора найти косинус того же угла, синус которого равен X.
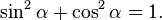
Затем, поделив синус на косинус, находим тангенс искомого угла, а затем, используя стандартную функцию арктангенса, и сам угол, который и будет искомым значением ArcSin(X).
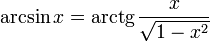
Борьба с погрешностью
С точки зрения математики, все действия проделаны корректно, кроме случаев X = ±1, приводящих к делению на 0, но и до того, как случится деление на 0, учитывая особенности машинного представления, имеет смысл находить арксинус другим путём, чтобы избегать стремящихся к бесконечности аргументов арктангенса. Разбиваем область определения арксинуса на центр, в котором производятся вычисления по выше приведённым формулам, и края. Разбить можно разными способами, но одно из способов разбиения примечательно тем, что аргументы, с которыми будет вызван ArcTan(X), будут не больше 1.0, что соответствует углу 45°, синус которого Sqrt(2)/2. Для правого края (Sqrt(2)/2 <= X <= 1) найдём арксинус другим способом: наоборот, поделим косинус (полученный по теореме Пифагора) на синус и получим котангенс, затем найдём угол, используя арккотангенс. Стандартной функции арккотангенса в Паскале нет, но арккотангенс очень просто выражается через арктангенс: ArcCot(X) := Pi/2 - ArcTan(X). Для левого края всё аналогично.
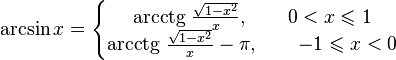
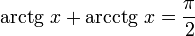
Реализация
function ArcSin(X: Real): Real;
begin
if X <= -1.0 then
ArcSin := -Pi / 2
else if X < -Sqrt(2) / 2 then
ArcSin := -Pi / 2 - ArcTan(Sqrt(1 - Sqr(X)) / X) { левый край }
else if X <= Sqrt(2) / 2 then
ArcSin := ArcTan(X / Sqrt(1 - Sqr(X))) { центр }
else if X < 1.0 then
ArcSin := Pi / 2 - ArcTan(Sqrt(1 - Sqr(X)) / X) { правый край }
else
ArcSin := Pi / 2
end;
begin
WriteLn(ArcSin(-1.0):0:3, ' ', ArcSin(-0.9):0:3, ' ',
ArcSin(0.3):0:3, ' ', ArcSin(0.9):0:3, ' ',
ArcSin(1.0):0:3);
{ -1.571 -1.120 0.305 1.120 1.1571 }
end.
::
::
::
